Factors of 1200 | Find the Factors of 1200 by Factoring Calculator
Created By : Jatin Gogia
Reviewed By : Rajasekhar Valipishetty
Last Updated : Apr 06, 2023
Factoring Calculator calculates the factors and factor pairs of positive integers.
Factors of 1200 can be calculated quickly with the help of Factoring Calculator i.e. 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 25, 30, 40, 48, 50, 60, 75, 80, 100, 120, 150, 200, 240, 300, 400, 600, 1200 positive integers that divide 1200 without a remainder.
Factors of 1200 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 25, 30, 40, 48, 50, 60, 75, 80, 100, 120, 150, 200, 240, 300, 400, 600, 1200. There are 30 integers that are factors of 1200. The biggest factor of 1200 is 1200.

Factors of 1200 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 25, 30, 40, 48, 50, 60, 75, 80, 100, 120, 150, 200, 240, 300, 400, 600, 1200
| 1200 | ||||||||||||
| 2 | 600 | |||||||||||
| 2 | 300 | |||||||||||
| 2 | 150 | |||||||||||
| 2 | 75 | |||||||||||
| 3 | 25 | |||||||||||
| 5 | 5 | |||||||||||
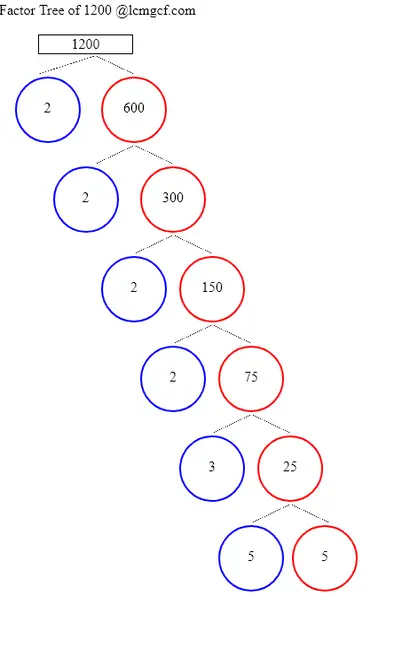
Factors of 1200 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 25, 30, 40, 48, 50, 60, 75, 80, 100, 120, 150, 200, 240, 300, 400, 600, 1200. There are 30 integers that are factors of 1200. The biggest factor of 1200 is 1200.
Positive integers that divides 1200 without a remainder are listed below.
Factors of 1200 List
- 1
- 2
- 3
- 4
- 5
- 6
- 8
- 10
- 12
- 15
- 16
- 20
- 24
- 25
- 30
- 40
- 48
- 50
- 60
- 75
- 80
- 100
- 120
- 150
- 200
- 240
- 300
- 400
- 600
- 1200
Factors of 1200 in pairs
- 1 × 1200 = 1200
- 2 × 600 = 1200
- 3 × 400 = 1200
- 4 × 300 = 1200
- 5 × 240 = 1200
- 6 × 200 = 1200
- 8 × 150 = 1200
- 10 × 120 = 1200
- 12 × 100 = 1200
- 15 × 80 = 1200
- 16 × 75 = 1200
- 20 × 60 = 1200
- 24 × 50 = 1200
- 25 × 48 = 1200
- 30 × 40 = 1200
- 40 × 30 = 1200
- 48 × 25 = 1200
- 50 × 24 = 1200
- 60 × 20 = 1200
- 75 × 16 = 1200
- 80 × 15 = 1200
- 100 × 12 = 1200
- 120 × 10 = 1200
- 150 × 8 = 1200
- 200 × 6 = 1200
- 240 × 5 = 1200
- 300 × 4 = 1200
- 400 × 3 = 1200
- 600 × 2 = 1200
- 1200 × 1 = 1200
Factors of 1200 Table
| Factor | Factor Number |
|---|---|
| 1 | one |
| 2 | two |
| 3 | three |
| 4 | four |
| 5 | five |
| 6 | six |
| 8 | eight |
| 10 | ten |
| 12 | twelve |
| 15 | fifteen |
| 16 | sixteen |
| 20 | twenty |
| 24 | twenty four |
| 25 | twenty five |
| 30 | thirty |
| 40 | forty |
| 48 | forty eight |
| 50 | fifty |
| 60 | sixty |
| 75 | seventy five |
| 80 | eighty |
| 100 | one hundred |
| 120 | one hundred twenty |
| 150 | one hundred fifty |
| 200 | two hundred |
| 240 | two hundred forty |
| 300 | three hundred |
| 400 | four hundred |
| 600 | six hundred |
| 1200 | one thousand two hundred |
How to find Factors of 1200?
As we know factors of 1200 are all the numbers that can exactly divide the number 1200 simply divide 1200 by all the numbers up to 1200 to see the ones that result in zero remainders. Numbers that divide without remainder are factors and in this case below are the factors
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 25, 30, 40, 48, 50, 60, 75, 80, 100, 120, 150, 200, 240, 300, 400, 600, 1200 are the factors and all of them can exactly divide number 1200.
Related Greatest Common Factors of 1200
Frequently Asked Questions on Factors of 1200
1. What are the factors of 1200?
Answer: Factors of 1200 are the numbers that leave a remainder zero. The ones that can divide 1200 exactly i.e. factors are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 25, 30, 40, 48, 50, 60, 75, 80, 100, 120, 150, 200, 240, 300, 400, 600, 1200.
2.What are Factor Pairs of 1200?
Answer:Factor Pairs of 1200 are
- 1 × 1200 = 1200
- 2 × 600 = 1200
- 3 × 400 = 1200
- 4 × 300 = 1200
- 5 × 240 = 1200
- 6 × 200 = 1200
- 8 × 150 = 1200
- 10 × 120 = 1200
- 12 × 100 = 1200
- 15 × 80 = 1200
- 16 × 75 = 1200
- 20 × 60 = 1200
- 24 × 50 = 1200
- 25 × 48 = 1200
- 30 × 40 = 1200
- 40 × 30 = 1200
- 48 × 25 = 1200
- 50 × 24 = 1200
- 60 × 20 = 1200
- 75 × 16 = 1200
- 80 × 15 = 1200
- 100 × 12 = 1200
- 120 × 10 = 1200
- 150 × 8 = 1200
- 200 × 6 = 1200
- 240 × 5 = 1200
- 300 × 4 = 1200
- 400 × 3 = 1200
- 600 × 2 = 1200
- 1200 × 1 = 1200
3. What is meant by Factor Pairs?
Answer:Factor Pairs are numbers that when multiplied together will result in a given product.