How to find LCM
Created By : Jatin Gogia
Reviewed By : Rajasekhar Valipishetty
Last Updated : Apr 06, 2023
Take the help of the online tool to Find LCM in a short span of time. You just need to input the data in the input fields and click on the calculate button next to the input section to avail the Least Common Multiple quickly.
Ex: LCM of 12, 48, 64 (or) LCM of 16, 56, 22 (or) LCM of 8, 72, 48
Here are some samples of LCM of Numbers calculations.

Related Calculators:
- LCD Calculator
- Least Common Denominator Calculator
- Greatest Common Divisor Calculator
- Greatest Common Factor Calculator
How to find LCM: Are you looking for ways on how to find the Least Common Multiple? Then you have landed on the right page and in this article of ours, we have listed several methods to find the LCM manually. In addition, you will learn about the definition of LCM, Solved examples for a better understanding of the concept. Get to know the step by step procedure involved for methods like Listing Multiples, Prime Factorization to find the Least Common Multiple or Least Common Denominator.
Least Common Multiple Definition
The Least Common Multiple is the smallest common multiple for two or more numbers. LCM is the Least Common Factor or multiple of two or more integers. It is denoted as LCM(a, b) for the integers a and b.
For Example, LCM of 16 and 20 is 80 as it the smallest multiple that is divisible by both the numbers.
How to find LCM(Least Common Multiple)?
There are numerous methods of finding the Least Common Multiple. Of all of them, we have a few popular methods explained along with examples showing with work. Choose the method that suits your level of understanding and find the Least Common Multiple easily. Have a glance at them and they are as such
- Listing Multiples
- Prime Factorization
- LCM Formula
- Least Common Multiple Tree
Steps to find LCM using Listing Multiples
- In order to find the LCM of given numbers firstly, you need to write the multiples of all the given numbers.
- Check for the common multiples among the multiples obtained.
- There might be instances where you will have more common multiples as we go on beyond.
- However, LCM is the smallest common multiple.
Example
Find the LCM of 4, 6
Solution:
Given Numbers are 4, 6
Multiples of 4 = 4, 8, 12, 16, 20, 24, 28...
Multiples of 6 = 6, 12, 18, 24, 30, 36...
12 and 24 are the common multiples found as far as we wrote the multiples
However, 12 is the smallest number common mong the multiples obtained, and thus it is the LCM of 4, 6
How to find LCM using Prime Factorization?
Another Prominent method to find the LCM is through Prime Factorisation. Go through the below steps to find the Least Common Multiple of Numbers using the Prime Factorization Method.
- Write down the Prime Factors of all the numbers given individually.
- After getting the Prime Factors, pair the Common Prime factors to get the Least Common Multiple.
Example
Find the LCM(12, 16, 18) using Prime Factorization?
Solution:
Given Inputs are 12, 16, 18
Prime Factorization of 12 = 2 x 2 x 3
Prime Factorization of 16 = 2 x 2 x 2 x 2
Prime Factorization of 18 = 2 x 2 x 2 x 3
Pairing the Common Prime Factors we get the LCM = 2 x 2 x 2 x 2 x 3 x 3
LCM(12, 16, 18) = 144
Therefore, LCM(12, 16, 18) is 144
Finding the Least Common Multiple using Formula
If you ever feel tedious to write down the multiples or go with the prime factorization method to find the Least Common Multiple we have got you the easiest way. Try finding the LCM using LCM Formula and get the result instantaneously.
Let us consider two integers a, b then we will get the formula depending on the GCD as such
LCM(a, b) = (a*b)/GCD(a, b)
The formula differs for Fractions and the LCM of Fractions is given as under
LCM of Fractions = L.C.M of Numerator/H.C.F of Denominator
Example
Find the LCM(11, 33) using the LCM Formula?
Solution:
Given Inputs are 11, 33
As per LCM Formula
LCM(a, b) = (a*b)/GCD(a, b)
Substitute the inputs in the formula we get the equation as such
LCM(11,33) = (11*33)/GCD(11,33)
GCD(11, 33) = 11 the highest number that divides both the numbers exactly
Substitute the GCD value in the above equation
LCM(11, 33) = (11*33)/11
LCM(11, 33) = 33
Therefore LCM(11,33) is 33
Procedure to find LCM using Least Common Multiple Trees
- You can frame the Least Common Multiple Trees using the Prime Factorization Method.
- Break down the given numbers in the form of multiples at first and then split them into prime factors.
- List out the Common Prime Factors and the Unique Factors from the branches of both the Numbers and multiply them to get the LCM.
Example
Find the LCM(60, 282) using the Least Common Multiples Trees?
Solution:
Given Input Numbers are 60, 282
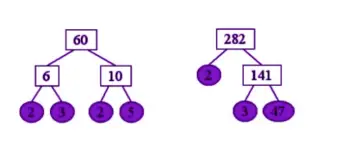
Bringing out the Common Factors Pairs and Unique Factors from the branches of both the numbers we will get the LCM
LCM = 2 x 2 x 3 x 5 x 47 = 2820
Therefore, LCM(60, 282) is 2820
FAQs on How to Find LCM
1. What is the fastest way to find the LCM?
Take the help of the LCM Calculator over here if you want accurate and faster results.
2. What are the different methods to find the Least Common Multiple?
Different methods to find the Least Common Multiple are as such.
- Listing Multiples
- Prime Factorization
- LCM Formula
- Least Common Multiple Tree
3. Which website offers a detailed procedure on how to find LCM?
lcmgcf.com is a trusted website that offers a detailed procedure on how to find the LCM.
4. What is the Formula of LCM?
Formula to find LCM of Numbers is LCM(a,b) = (a*b)/GCD(a,b).