LCM of 3 Numbers Calculator

The Least Common Multiple is the smallest integer that is divisible by all the numbers. For three integers a, b, c LCM is denoted as LCM(a, b, c). It is also known as LCD or Least Common Denominator.

For instance LCM of 12, 15, 10 is 60 the smallest number that is divisible by all three numbers. Therefore LCM(12, 15, 10) = 60.

Procedure to find the Least Common Multiple of 3 Numbers

Check out the manual procedure on how to find LCM of 3 numbers by hand using different techniques. Each of the methods is explained using step by step process along with solved examples. Understand the concept better and choose the method that is convenient for you. If you feel any difficulty They are along the lines

• Listing Multiples
• Prime Factorization
• Cake/Ladder Method
• Division Method
• Using the Greatest Common Factor GCF

LCM of 3 Numbers using Listing Multiples

• List all the multiples of 3 numbers till you have at least one of the multiples appear on all the lists.
• Find the number that is the smallest and is present on all the lists.
• That itself is the Least Common Multiple of the numbers.

Example

Find LCM(6, 7, 21) using Listing Multiples?

Solution:

Given numbers are 6, 7, 21

Multiples of 6 are 6, 12, 18, 24, 30, 36, 42, 48, 54, 60.

Multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56

Multiples of 21 are 21, 42, 63

As per the definition, LCM is the smallest number that is common in all 3 numbers multiples.

Thus, 42 is the LCM of 6, 7, 21.

LCM of Three Numbers using Prime Factorization

• Make a note of all the Prime Factors of the given numbers.
• List all the prime numbers found as many times they occur often for the given numbers.
• Multiply the list of prime numbers to obtain the Least Common Multiple.

Example

Find LCM of 12, 24, 30 using Prime Factorization?

Solution:

Prime Factorization of 12 = 2 × 2 × 3

Prime Factorization of 24 = 2 × 2 × 2 × 3

Prime Factorization of 30 = 2 × 3 × 5

Make a note of prime numbers that occur often for the given numbers and multiply them

= 2×2×2×3×5

= 120

How to find LCM of 3 Numbers using the Cake/ Ladder Method?

The cake or Ladder Method is the easiest method to find the Least Common Multiple of all the methods. Go through the procedure below

• Write down all the 3 numbers in a cake or row.
• Divide the numbers in the layer with a prime number that is evenly divisible in two or more numbers and bring the result into the next layer.
• If any number in the layer or row isn't divisible just bring it down.
• Continue dividing rows by prime numbers.
• When there are no more prime numbers that divide evenly two or more numbers you are done.

Example

Find the LCM(10, 12, 15) using the Cake/ Ladder Method?

Solution:

Given Numbers are 10, 12, 15

To find LCM Multiply all the prime numbers from top to bottom i.e. 2*3*5*1*2*1

= 60

Therefore, LCM(10, 12, 15) is 60

If you are looking for help on finding the LCM, GCF concepts you can always visit the portal lcmgcf.com to clear all your queries.

Steps to find LCM of 3 Numbers using the Division Method?

• Write down all the numbers in a top table row.
• Begin with the Lowest Prime Numbers and divide the numbers of row by prime numbers that are evenly divisible into at least one of the numbers and bring it to the next row.
• If any number is not divisible bring it down.
• Continue dividing with Prime Numbers that divide at least one number.
• When the last rows are 1's you are done.

Example

Find LCM of 10, 18, 25 using the Division Method?

Solution:

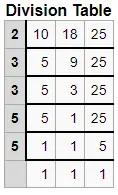
LCM is the Product of Prime Numbers in the first column

LCM = 2 × 3 × 3 × 5 × 5

LCM = 450

Therefore, LCM(10, 18, 25) is 450.

Finding LCD of 3 Numbers using GCF?

• Initially, find the LCM of the first two numbers.
• Later, find the LCM of the result obtained for the first two numbers and the third number.
• This way, you can find the Least Common Multiple of 3 Numbers easily.

Example

Find the LCM(12, 24, 36) using the GCF Method?

Solution:

Given Numbers are 12, 24, 36

Step 1:Find the LCM of the first 2 numbers 12, 24

LCM of 12, 24 is 24 the smallest number that is divisible by both the numbers.

Step 2: Now take the LCM of the result i.e. 24, 36

LCM(24, 36) = 72

72 is the smallest number that is divisible by both the numbers.

Therefore, the LCM(12, 24, 36) is 72.

1. What does LCM Stand for?

LCM Stands for Least Common Multiple. It is also known as the Least Common Denominator or LCD.

2. What is meant by Least Common Multiple?

The Least Common Multiple is the smallest integer that is divisible by all the numbers.

3. What are the different methods to find LCM?

There are five different methods to find LCM and they are as such

• Listing Multiples
• Prime Factorization
• Cake/Ladder Method
• Division Method
• Using the Greatest Common Factor GCF

4. How to find LCM of 3 numbers using a Calculator?

Simply provide the inputs in the input field and click on the calculate button to get the Least Common Multiple along with detailed work in no time.