Prime Factorisation Calculator
Created By : Jatin Gogia
Reviewed By : Rajasekhar Valipishetty
Last Updated : Apr 06, 2023
Prime Factorisation Calculator used to calculate the prime factorisation of the number you enter here. (Numbers above 10 million may or may not time out. When you have to find out the Prime Factorisation of very large numbers, the Prime Factorisation Calculator can be very handy and useful.
Please type a positive integer number and hit 'Calculate Factors' button find the prime factors.
Ex: Prime Factors of 25 (or) Prime Factors of 46 (or) Prime Factors of 57
Here are some samples of Prime Factorisation calculations.

Related Calculators:
Table of Factors from 1 to 100
| Number | Factors | Prime or Composite |
| 1 | 1 | Neither prime nor composite |
| 2 | 1, 2 | Prime |
| 3 | 1, 3 | Prime |
| 4 | 1, 2, 4 | Composite |
| 5 | 1, 5 | Prime |
| 6 | 1, 2, 3, 6 | Composite |
| 7 | 1, 7 | Prime |
| 8 | 1, 2, 4, 8 | Composite |
| 9 | 1, 3, 9 | Composite |
| 10 | 1, 2, 5, 10 | Composite |
| 11 | 1, 11 | Prime |
| 12 | 1, 2, 3, 4, 6, 12 | Composite |
| 13 | 1, 13 | Prime |
| 14 | 1, 2, 7, 14 | Composite |
| 15 | 1, 3, 5, 15 | Composite |
| 16 | 1, 2, 4, 8, 16 | Composite |
| 17 | 1, 17 | Prime |
| 18 | 1, 2, 3, 6, 9, 18 | Composite |
| 19 | 1, 19 | Prime |
| 20 | 1, 2, 4, 5, 10, 20 | Composite |
| 21 | 1, 3, 7, 21 | Composite |
| 22 | 1, 2, 11, 22 | Composite |
| 23 | 1, 23 | Prime |
| 24 | 1, 2, 3, 4, 6, 8, 12, 24 | Composite |
| 25 | 1, 5, 25 | Composite |
| 26 | 1, 2, 13, 26 | Composite |
| 27 | 1, 3, 9, 27 | Composite |
| 28 | 1, 2, 4, 7, 14, 28 | Composite |
| 29 | 1, 29 | Prime |
| 30 | 1, 2, 3, 5, 6, 10, 15, 30 | Composite |
| 31 | 1, 31 | Prime |
| 32 | 1, 2, 4, 8, 16, 32 | Composite |
| 33 | 1, 3, 11, 33 | Composite |
| 34 | 1, 2, 17, 34 | Composite |
| 35 | 1, 5, 7, 35 | Composite |
| 36 | 1, 2, 3, 4, 6, 9, 12, 18, 36 | Composite |
| 37 | 1, 37 | Prime |
| 38 | 1, 2, 19, 38 | Composite |
| 39 | 1, 3, 13, 39 | Composite |
| 40 | 1, 2, 4, 5, 8, 10, 20, 40 | Composite |
| 41 | 1, 41 | Prime |
| 42 | 1, 2, 3, 6, 7, 14, 21, 42 | Composite |
| 43 | 1, 43 | Prime |
| 44 | 1, 2, 4, 11, 22, 44 | Composite |
| 45 | 1, 3, 5, 9, 15, 45 | Composite |
| 46 | 1, 2, 23, 46 | Composite |
| 47 | 1, 47 | Prime |
| 48 | 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 | Composite |
| 49 | 1, 7, 49 | Composite |
| 50 | 1, 2, 5, 10, 25, 50 | Composite |
| 51 | 1, 3, 17, 51 | Composite |
| 52 | 1, 2, 4, 13, 26, 52 | Composite |
| 53 | 1, 53 | Prime |
| 54 | 1, 2, 3, 6, 9, 18, 27, 54 | Composite |
| 55 | 1, 5, 11, 55 | Composite |
| 56 | 1, 2, 4, 7, 8, 14, 28, 56 | Composite |
| 57 | 1, 3, 19, 57 | Composite |
| 58 | 1, 2, 29, 58 | Composite |
| 59 | 1, 59 | Prime |
| 60 | 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 | Composite |
| 61 | 1, 61 | Prime |
| 62 | 1, 2, 31, 62 | Composite |
| 63 | 1, 3, 7, 9, 21, 63 | Composite |
| 64 | 1, 2, 4, 8, 16, 32, 64 | Composite |
| 65 | 1, 5, 13, 65 | Composite |
| 66 | 1, 2, 3, 6, 11, 22, 33, 66 | Composite |
| 67 | 1, 67 | Prime |
| 68 | 1, 2, 4, 17, 34, 68 | Composite |
| 69 | 1, 3, 23, 69 | Composite |
| 70 | 1, 2, 5, 7, 10, 14, 35, 70 | Composite |
| 71 | 1, 71 | Prime |
| 72 | 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72 | Composite |
| 73 | 1, 73 | Prime |
| 74 | 1, 2, 37, 74 | Composite |
| 75 | 1, 3, 5, 15, 25, 75 | Composite |
| 76 | 1, 2, 4, 19, 38, 76 | Composite |
| 77 | 1, 7, 11, 77 | Composite |
| 78 | 1, 2, 3, 6, 13, 26, 39, 78 | Composite |
| 79 | 1, 79 | Prime |
| 80 | 1, 2, 4, 5, 8, 10, 16, 20, 40, 80 | Composite |
| 81 | 1, 3, 9, 27, 81 | Composite |
| 82 | 1, 2, 41, 82 | Composite |
| 83 | 1, 83 | Prime |
| 84 | 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84 | Composite |
| 85 | 1, 5, 17, 85 | Composite |
| 86 | 1, 2, 43, 86 | Composite |
| 87 | 1, 3, 29, 87 | Composite |
| 88 | 1, 2, 4, 8, 11, 22, 44, 88 | Composite |
| 89 | 1, 89 | Prime |
| 90 | 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90 | Composite |
| 91 | 1, 7, 13, 91 | Composite |
| 92 | 1, 2, 4, 23, 46, 92 | Composite |
| 93 | 1, 3, 31, 93 | Composite |
| 94 | 1, 2, 47, 94 | Composite |
| 95 | 1, 5, 19, 95 | Composite |
| 96 | 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96 | Composite |
| 97 | 1, 97 | Prime |
| 98 | 1, 2, 7, 14, 49, 98 | Composite |
| 99 | 1, 3, 9, 11, 33, 99 | Composite |
| 100 | 1, 2, 4, 5, 10, 20, 25, 50, 100 | Composite |
The prime factorisation calculator can help you to find prime factors of any integer number up to 1 trillion. Just enter the number here in the calculator and within no time you’ll get the prime factorisation.
Prime Factorisation Calculator various applications:
- Check Prime factors of an integer number up to 1 trillion
- Also, it can check either a number is prime or not
- Prime decomposition in an exponential way
- Make a list of all positive prime numbers smaller than the number you entered and calculate them
- Comma-separated Values (CSV) of prime factors
To know the complete process, first of all, you must know all about what is a prime number?
A prime number is a positive whole number that is greater than 1 and that can be divided equally just by one and by itself. We can also say that cannot be achieved by multiplying 2 smaller numbers than that. Like 7 is a prime number! You can divide it by 1 or 7 only.
if an integer number is small then it’s very simple to decide whether a number is prime or not. For small numbers, we can use the rules of divisibility and trial division manually. But what if a number is very large and we have to determine whether it is prime or not. It is hard to check it manually as factoring large numbers carry very large primes. In such situations, an online calculator is the best to choose.
What is the prime factor?
Factors of prime numbers are prime factors. So here if we consider the factors of 12, that is, we need to get what integer numbers multiply to provide you 12. We understand that 1 x 12 = 12, 2 x 6 = 12 and 3 x 4 = 12. But here 12, 6, and 4 are not prime factors. The only prime factors of 12 are 2 and 3. You can also check prime factors using a factor calculator.
What is Prime Factorisation?
Any whole number can be uniquely described as the list of prime numbers and such representation is named the prime factorisation, or canonical representation or integer factorisation or prime decomposition. There is exactly one prime factorisation for any positive integer number, and such positive integer has just 1 prime factorisation.
How to Find Prime Factorisation of a Number?
There are various processes to find out the Prime Factorisation of a Number and you can choose any of one as per the need. Here, we try to include two of the methods of prime factorisation:
Trial Division
One of the methods to check the Prime Factor of a number is trial division. Trial division consists of very easy and basic algorithms, though it is an extremely slow process. In this method, we have to check each number by dividing the composite number in question by the integer and deciding if, and how many times, the number can divide the number equally.
To make it more understandable, let go through an example:
To get the prime factorisation of 48, we have to start with dividing it by the smallest prime 2
48 ÷ 2 = 24
24 ÷ 2 = 12
12 ÷ 2 = 6
6 ÷ 2 = 3
But, we can’t divide 3 by 2, but we can divide 3 by itself only
3 ÷ 3 = 1
So here he prime factorisation of 48 = 2 X 2 X 2 X 2 X 3 = 24 X 3
We can check it in a prime factorisation calculator also. The algorithm used in the calculator and trial division may differ but the result is always the same.
Prime Decomposition
Another popular method to find prime factorisation is known as prime decomposition and it includes the use of a factor tree. The factor tree diagram is an easy process to divide a number into its prime factors. To create a factor tree we have to break down the composite number into factors of the composite number till the numbers are prime.
There might be various methods to show the factor tree for any provided prime factorisation.
Here let’s take an example of 48 to check the prime factor using prime decomposition method.
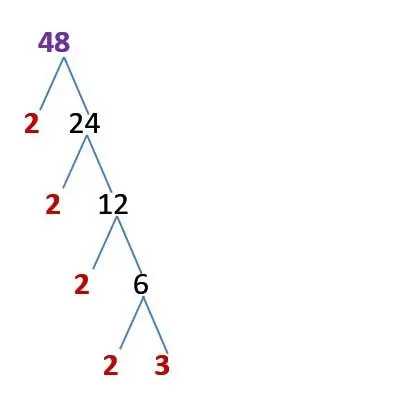
It doesn’t matter whether you are using a calculator or find yourself, the factorisation will be unique always. And when there are very big numbers, the calculator is much more amazing!
Examples of Prime Decomposition: Factors and Exponents
- Prime factorization of 100 is 2 x 2 x 5 x 5 or 22 x 52
- Prime factorization of 76 is 2 x 2 x 19 or 22 x 191
- Prime factorization of 50 is 2 x 5 x 5 or 2 x 52
- Prime factorization of 48 is 2 x 2 x 2 x 2 x 3 or 24 x 31
- Prime factorization of 36 is 2 x 2 x 3 x 3 or 22 x 32
- Prime factorization of 20 is 2 x 2 x 5 or 22 x 51
- Prime factorization of 10 is 2 x 5 or 21 x 51
Prime Factorisation Calculator is made by the team of lcmgcf.com to enhance your knowledge about the concepts and make it easier to understand the solution step by step.
Prime Factors Calcualtor Examples
- Prime Factors of 40
- Prime Factors of 96
- Prime Factors of 43
- Prime Factors of 21
- Prime Factors of 87
- Prime Factors of 108
- Prime Factors of 2160
- Prime Factors of 51
- Prime Factors of 55
- Prime Factors of 3125
- Prime Factors of 900
- Prime Factors of 420
- Prime Factors of 26
- Prime Factors of 49
- Prime Factors of 1331
- Prime Factors of 300
- Prime Factors of 1620
- Prime Factors of 162
- Prime Factors of 400
- Prime Factors of 1728
- Prime Factors of 27000
- Prime Factors of 2401
- Prime Factors of 24
- Prime Factors of 243
- Prime Factors of 92
- Prime Factors of 315
- Prime Factors of 63
- Prime Factors of 1764
- Prime Factors of 8281
- Prime Factors of 112
- Prime Factors of 2025
- Prime Factors of 630
- Prime Factors of 41
- Prime Factors of 78
- Prime Factors of 91
- Prime Factors of 504
- Prime Factors of 58
- Prime Factors of 99
- Prime Factors of 69
- Prime Factors of 2645
- Prime Factors of 100
- Prime Factors of 74
- Prime Factors of 2000
- Prime Factors of 97
- Prime Factors of 50
- Prime Factors of 70
- Prime Factors of 1008
- Prime Factors of 468
- Prime Factors of 115
- Prime Factors of 34
- Prime Factors of 168
- Prime Factors of 95
- Prime Factors of 1296
- Prime Factors of 1156
- Prime Factors of 180
- Prime Factors of 62
- Prime Factors of 198
- Prime Factors of 154
- Prime Factors of 150
- Prime Factors of 160
- Prime Factors of 3969
- Prime Factors of 143
- Prime Factors of 153
- Prime Factors of 156
- Prime Factors of 1849
- Prime Factors of 4913
- Prime Factors of 2744
- Prime Factors of 841
- Prime Factors of 44
- Prime Factors of 81
- Prime Factors of 56
- Prime Factors of 221
- Prime Factors of 625
- Prime Factors of 114
- Prime Factors of 2197
- Prime Factors of 252
- Prime Factors of 1250
- Prime Factors of 176
- Prime Factors of 29
- Prime Factors of 165
- Prime Factors of 20
- Prime Factors of 600
- Prime Factors of 1000
- Prime Factors of 27
- Prime Factors of 336
- Prime Factors of 1369
- Prime Factors of 1323
- Prime Factors of 101
- Prime Factors of 7921
- Prime Factors of 132
- Prime Factors of 270
- Prime Factors of 126
- Prime Factors of 648
- Prime Factors of 89
- Prime Factors of 512
- Prime Factors of 273
- Prime Factors of 127
- Prime Factors of 110
- Prime Factors of 490
- Prime Factors of 391
- Prime Factors of 289
- Prime Factors of 432
- Prime Factors of 124
- Prime Factors of 75
- Prime Factors of 82
- Prime Factors of 2457
- Prime Factors of 140
- Prime Factors of 85
- Prime Factors of 999
- Prime Factors of 588
- Prime Factors of 5832
- Prime Factors of 125
- Prime Factors of 53
- Prime Factors of 5005
- Prime Factors of 529
- Prime Factors of 136
- Prime Factors of 59
- Prime Factors of 2010
- Prime Factors of 924
- Prime Factors of 455
- Prime Factors of 527
- Prime Factors of 5184
- Prime Factors of 1009
- Prime Factors of 1001
- Prime Factors of 39
- Prime Factors of 1872
- Prime Factors of 33150
- Prime Factors of 288
- Prime Factors of 4860
- Prime Factors of 25
- Prime Factors of 128
- Prime Factors of 1800
- Prime Factors of 147
- Prime Factors of 7744
- Prime Factors of 540
- Prime Factors of 220
- Prime Factors of 5431
- Prime Factors of 325
- Prime Factors of 343
- Prime Factors of 208
- Prime Factors of 46
- Prime Factors of 437
- Prime Factors of 1517
- Prime Factors of 152
- Prime Factors of 2020
- Prime Factors of 1225
- Prime Factors of 45
- Prime Factors of 133
- Prime Factors of 405
- Prime Factors of 2800
- Prime Factors of 4851
- Prime Factors of 5929
- Prime Factors of 2100
- Prime Factors of 187
- Prime Factors of 210
- Prime Factors of 2601
- Prime Factors of 175
- Prime Factors of 330
- Prime Factors of 693
- Prime Factors of 375
- Prime Factors of 1599
- Prime Factors of 216
- Prime Factors of 576
- Prime Factors of 19
- Prime Factors of 1458
- Prime Factors of 195
- Prime Factors of 250
- Prime Factors of 320
- Prime Factors of 22
- Prime Factors of 76
- Prime Factors of 225
- Prime Factors of 189
- Prime Factors of 1024
- Prime Factors of 1260
- Prime Factors of 729
- Prime Factors of 196
- Prime Factors of 30
- Prime Factors of 1591
- Prime Factors of 310
- Prime Factors of 403
- Prime Factors of 2021
- Prime Factors of 6000
- Prime Factors of 676
- Prime Factors of 1575
- Prime Factors of 323
- Prime Factors of 462
- Prime Factors of 720
- Prime Factors of 3375
- Prime Factors of 657
- Prime Factors of 120
- Prime Factors of 130
- Prime Factors of 222
- Prime Factors of 111
- Prime Factors of 319
- Prime Factors of 1125
- Prime Factors of 2250
- Prime Factors of 245
- Prime Factors of 182
- Prime Factors of 77
- Prime Factors of 430
FAQs on Prime Factorisation Calculator
Question 1: What is Prime Factorisation?
Answer 1: Prime factorisation means getting all the prime numbers that are factors of a number.
Question 2: What is The Sieve of Eratosthenes?
Answer 2: Eratosthenes invented a sieve to find prime numbers. It generally removes composite numbers and keeps prime numbers.
Question 3: What is a Composite Number?
Answer 3: When an integer number has more than two factors it is known as a composite number.
Question 4: Why find Prime Factors?
Answer 4: Prime Numbers can not be broken down so they are the basic blocks of all numbers. and this can be very helpful when working with large numbers, like in Cryptography.